Lecture 10 | Indexing#
Basic Concepts#
Indexing mechanisms used to speed up access to desired data.
索引用来加速查找。
Search Key - attribute to set of attributes used to look up records in a file.
An index file consists of records (called index entries) of the form.
索引文件通常是有顺序的
Index Evaluation Metrics#
- Access types supported efficiently
- Point query: records with a specified value in the attribute.
点查询 - Range query: records with an attribute value falling in a specified range of values.
范围查询
- Point query: records with a specified value in the attribute.
- Access time
- Insertion time
- Deletion time
- Space overhead
Ordered Indices#
- Primary index(主索引): in a sequentially ordered file, the index whose search key specifies the sequential order of the file.
- Also called clustering index(聚集索引)
- The search key of a primary index is usually but not necessarily the primary key.
- Secondary index(辅助索引): an index whose search key specifies an order different from the sequential order of the file. Also called non-clustering index.
Example
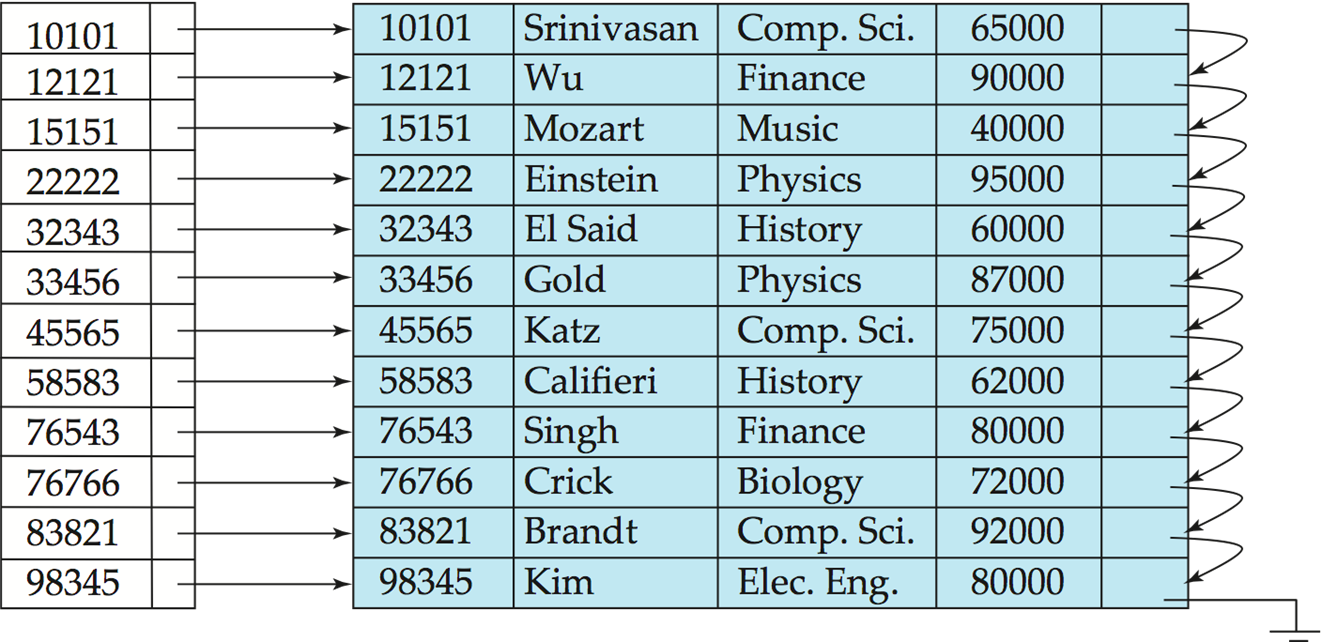
主索引和数据内的顺序是一样的。点查和范围查都是比较高效的。
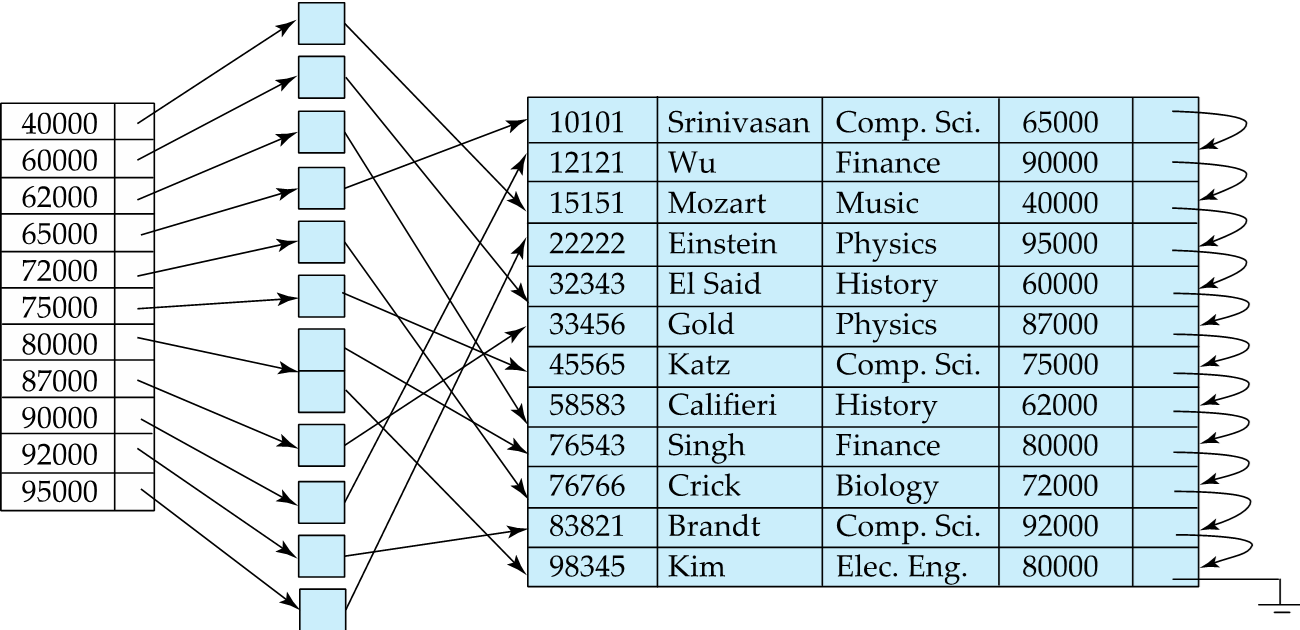
如果 key 不是一个主键,那可能会对应多个记录。
Primary index 是很宝贵的,只能有一个,其他都是辅助索引。
- Dense index(稠密索引) — Index record appears for every search-key value in the file.
所有 search-key 都要出现在索引文件里。 - Sparse Index(稀疏索引): contains index records for only some search-key values.
Example
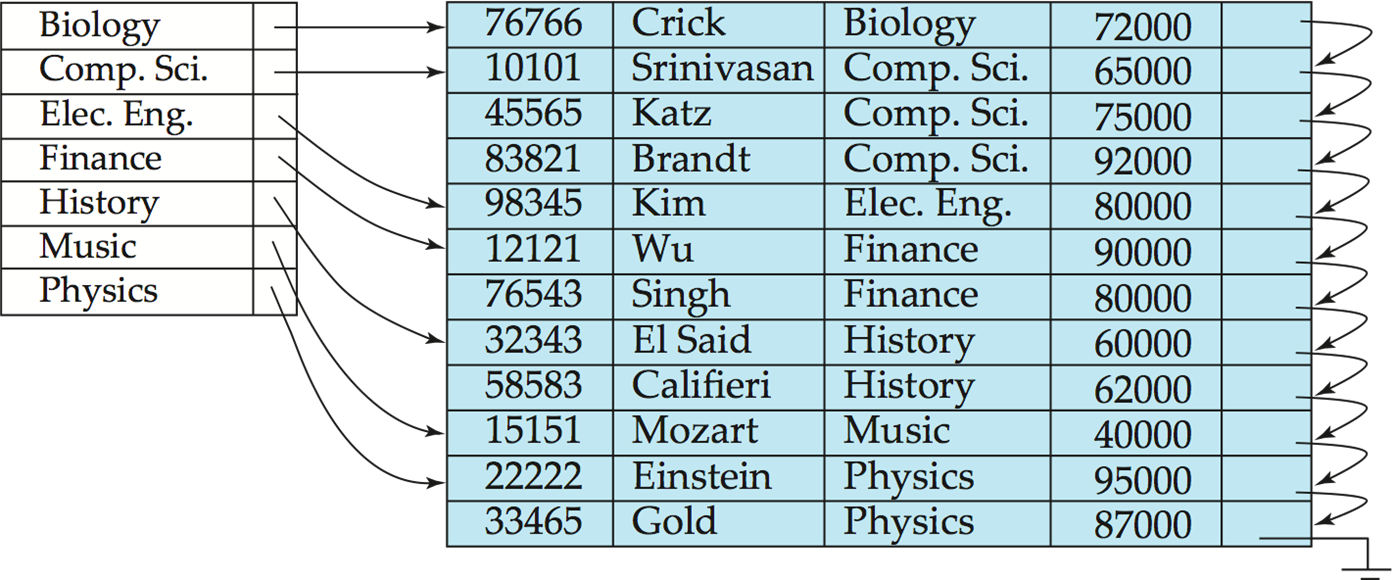

Good tradeoff: sparse index with an index entry for every block in file, corresponding to least search-key value in the block.

Multilevel Index#
If primary index does not fit in memory, access becomes expensive.
可以对索引文件本身再建立一次索引。
B+-Tree Index#
- All paths from root to leaf are of the same length
- Inner node(not a root or a leaf): between \(\lceil n/2\rceil\) and \(n\) children.
- Leaf node: between \(\lceil (n–1)/2\rceil\) and \(n–1\) values
- Special cases:
- If the root is not a leaf:
at least 2 children. - If the root is a leaf :
between 0 and (n–1)values.
- If the root is not a leaf:
一般一个节点就是一个块的大小, 4K.
B+ 树的叉是非常大的。
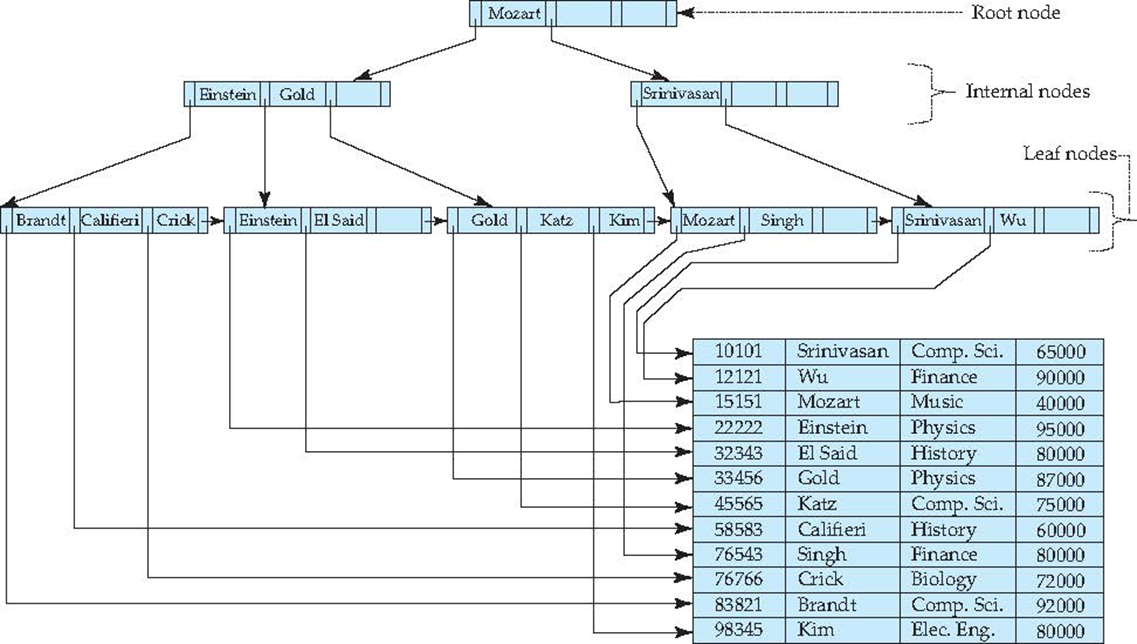
Observations about B+-trees#
Since the inter-node connections are done by pointers, “logically” close blocks need not be “physically” close. 如果有很多文件一次性建立 B+ 树,我们可以从叶子节点开始建立。
如果有 K 个索引项,则树高度不会超过 \(\lceil \log_{\lceil n/2 \rceil}(K/2)\rceil + 1\).
高度最小为 \(\log_n(K)\)
Examples of Insert on B+-Tree
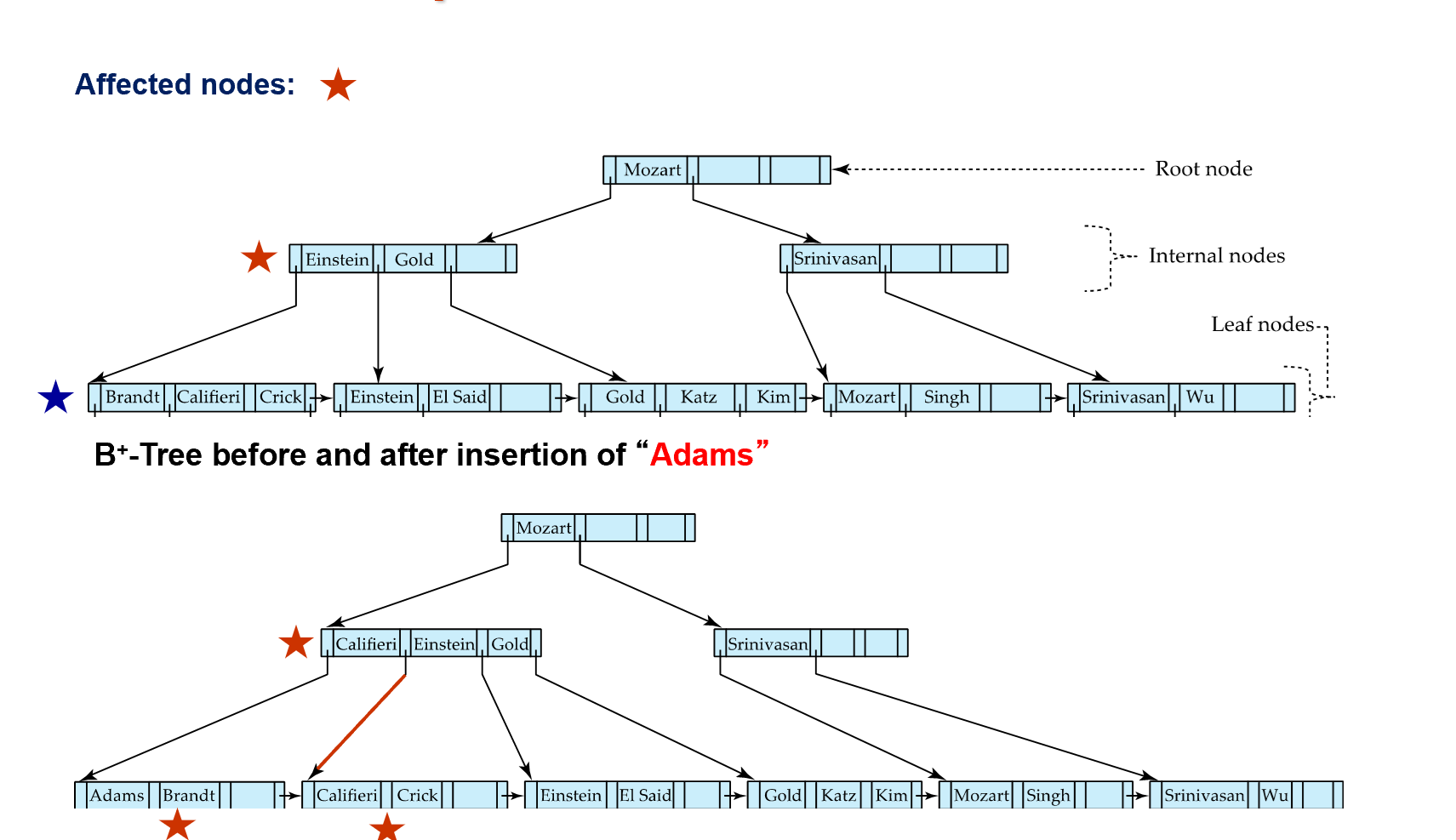
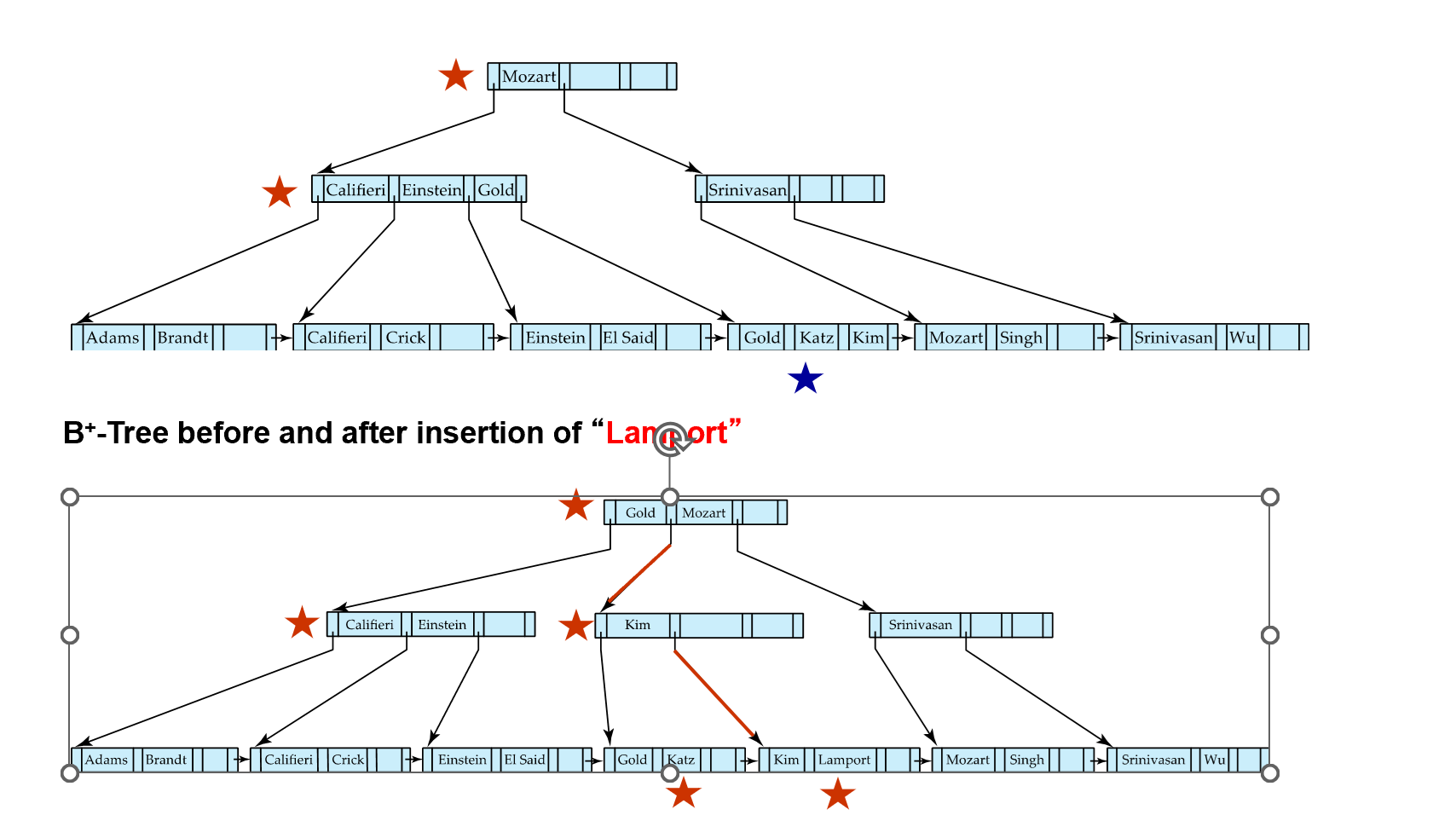
注意内点的 split 和叶子的不一样。要把中间的节点 move 上去。
Examples of Delete on B+-Tree

中间点如果不够,从另外一边借一个过来。但是不能直接借,需要把它顶上去。
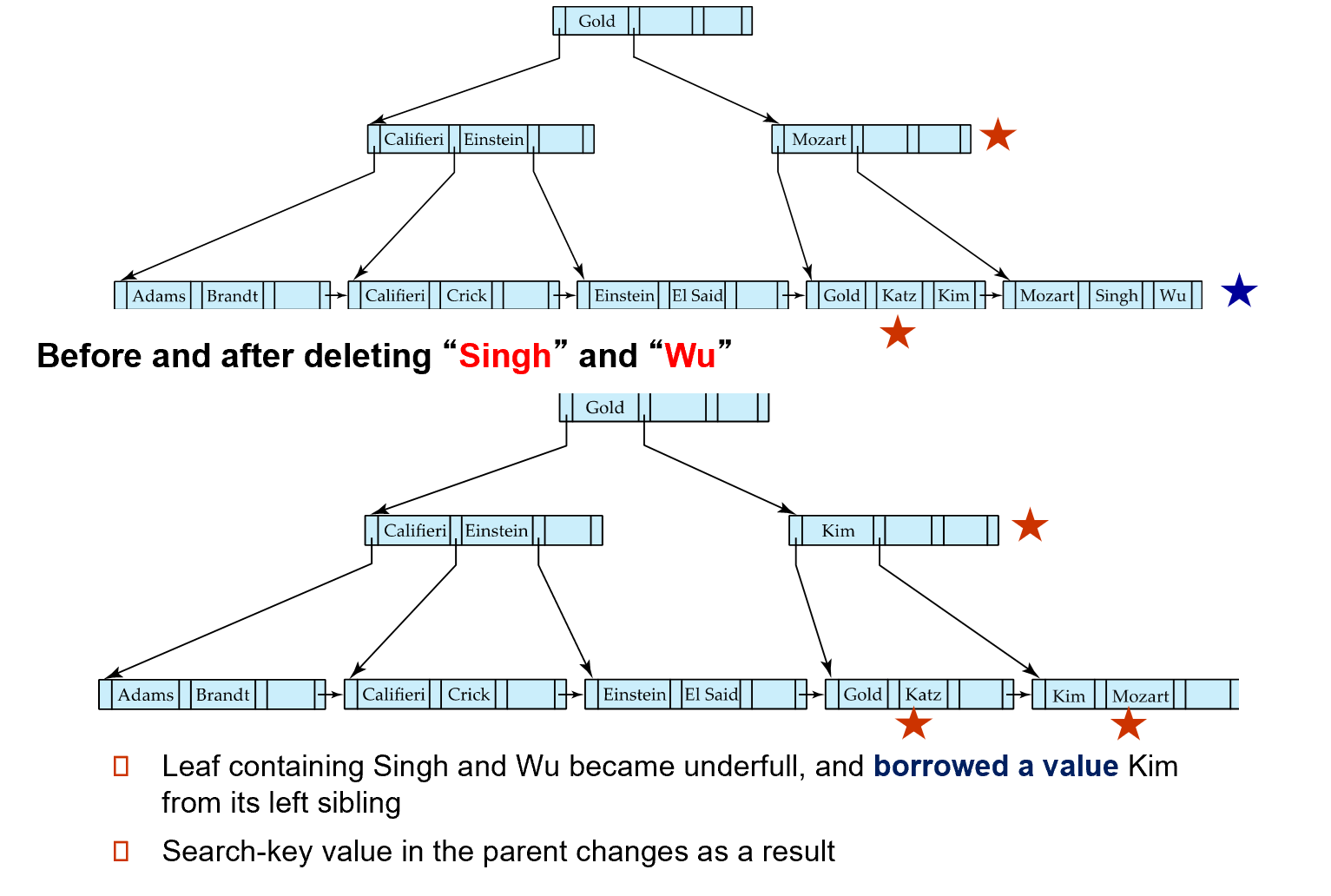
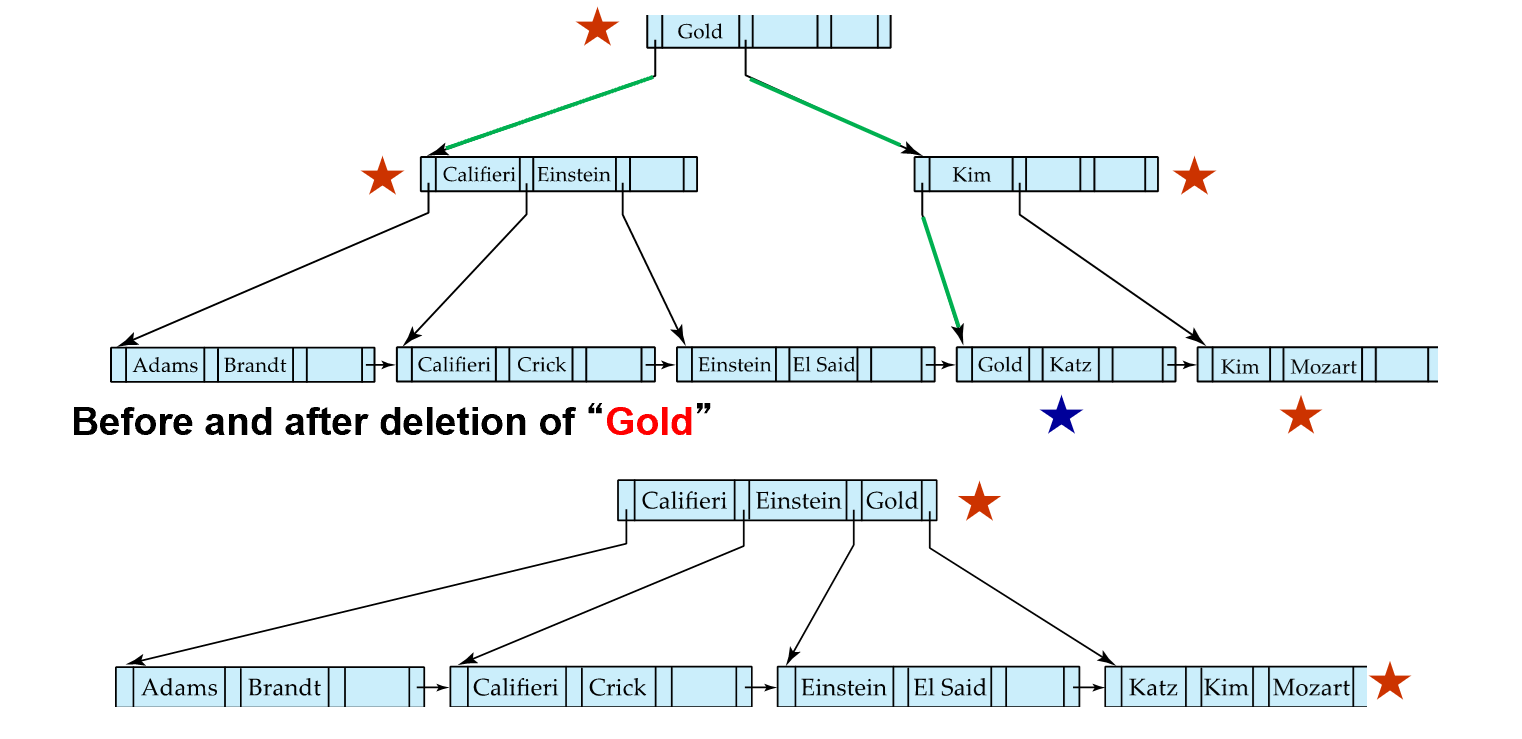
注意考虑和兄弟合并。
B+- tree : height and size estimation#


全满的时候节点最少
注意这里的向上/向下取整问题
浅层节点个数少,我们可以把第一层和第二层的节点都放到内存中 pin 住。
B+-Tree File Organization#
文件组织
B+-Tree File Organization:
- Leaf nodes in a B+-tree file organization store records, instead of pointers
叶子节点不再放索引项,放记录本身。 - Helps keep data records clustered even when there are insertions/deletions/updates
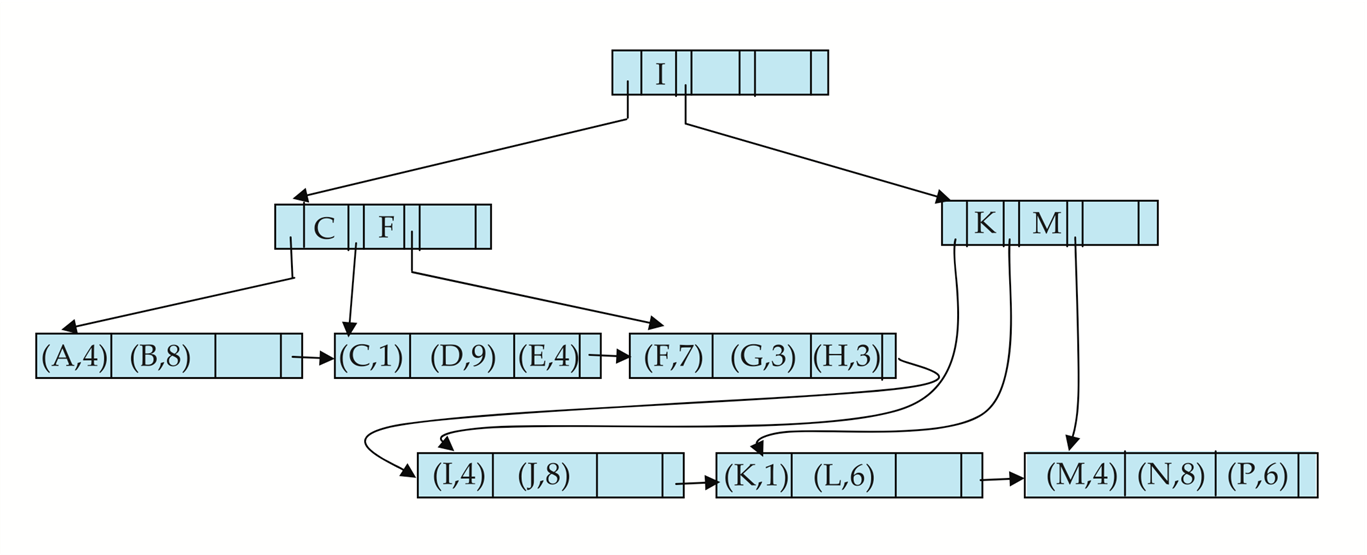
我们可以改变半满的要求以提高空间利用率。
Other Issues in Indexing#
- Record relocation and secondary indices
If a record moves, all secondary indices that store record pointers have to be updated
Node splits in B+-tree file organizations become very expensive
Solution: use primary-index search key instead of record pointer in secondary index - Variable length strings as keys
Variable fanout - Prefix compression
Key values at internal nodes can be prefixes of full key
Keep enough characters to distinguish entries in the subtrees separated by the key value
Multiple-Key Access#
Composite search keys are search keys containing more than one attribute
e.g. (dept_name, salary)
Lexicographic ordering: \((a_1, a_2) < (b_1, b_2)\) if either \(a_1 < b_1\), or \(a_1=b_1\) and \(a_2 < b_2\).
单个 key, 不同 key 之间组合都可以建立 B+ 树。这样会有很多组合,可以在频繁出现的查询属性上建立 B+ 树。
Non-unique Search Keys#
我们可以在 B+ 树叶子节点不直接指向磁盘里的数据,而是指向一个块。
也可以在索引上加上去一个索引,使它对应的记录唯一。
可以通过范围查找
Bulk Loading and Bottom-Up Build#
Inserting entries one-at-a-time into a B+-tree requires \(\geq 1\) IO per entry
如果我们一次性插入很多索引项
- Efficient alternative 1: Insert in sorted order
局部性较好,减少 I/O. - Efficient alternative 2: Bottom-up B+-tree construction
- First sort index entries
- Then create B+-tree layer-by-layer, starting with leaf level
- The built B+-tree is written to disk using sequential I/O operations
Example

如果要排序的内容较大,无法放下内存,可以使用外部排序。
fanout 可以计算出来。
可以用 level-order 写到磁盘里,便于顺序访问所有索引,此时块是连续的。(便于顺序访问所有数据项)
这里的代价就是建好后,一次 seek 后全部写出去 (9 blocks)
Bulk insert index entries
Example
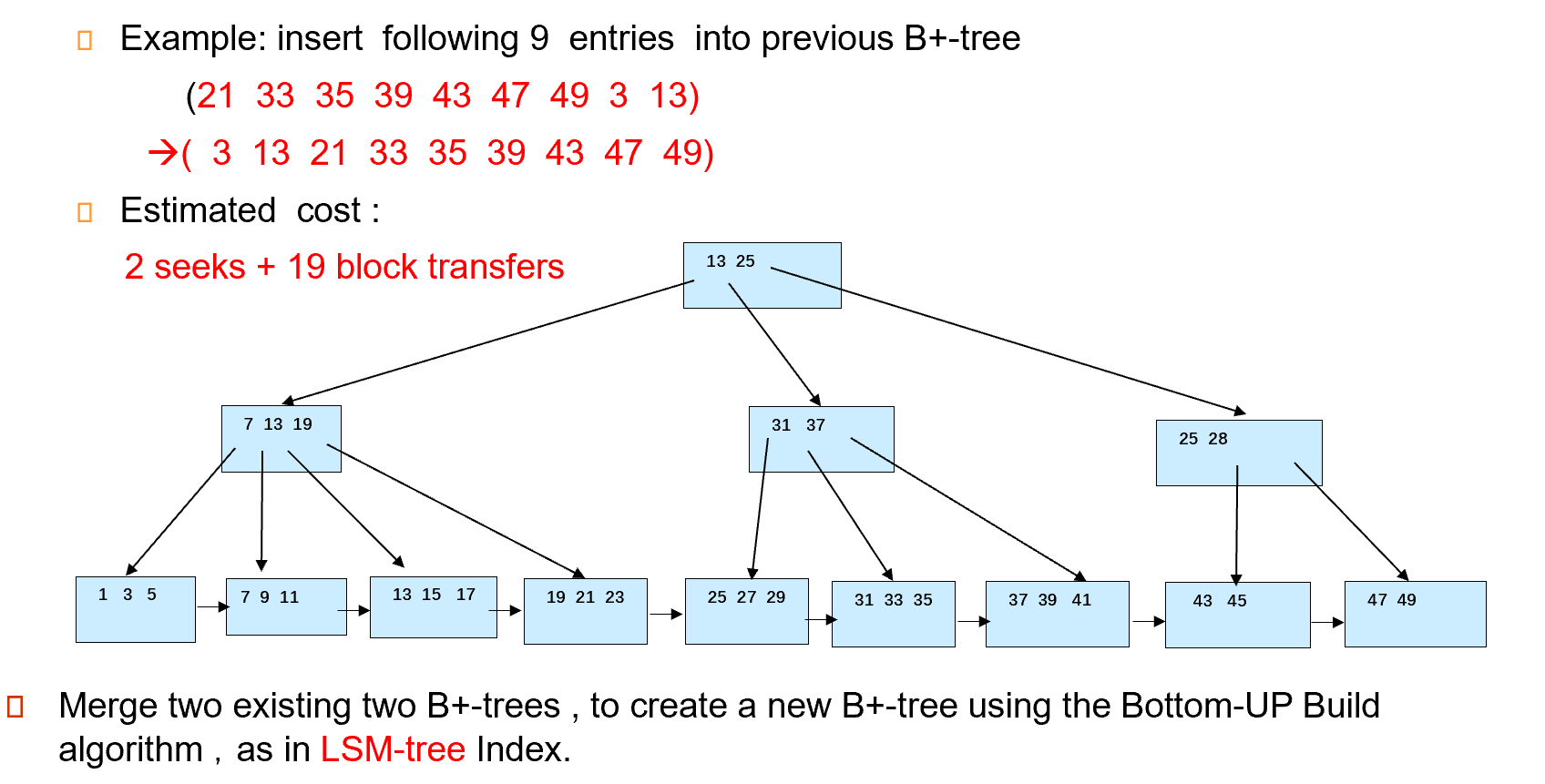
把刚刚那棵 B+ 树叶子节点(即遍历所有数据)需要 1seek+6blocks. 随后和上面的数据合并后,写回磁盘时需要 1seek+13blocks.
Merge two existing two B+-trees , to create a new B+-tree using the Bottom-UP Build algorithm, as in LSM-tree Index
假设有两棵这样生成的 B+ 树,将他们合并在一起。首先把叶子节点拿出来排序。
Indexing in Main Memory#
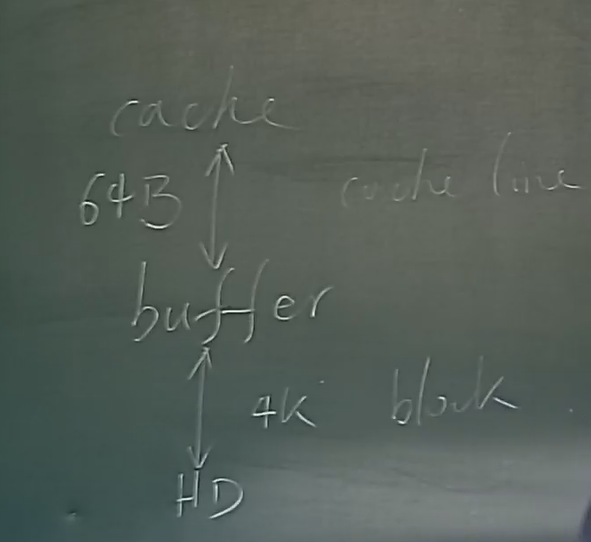
cache 按 cache line 传输, 只有 64B.
- Random access in memory
- Much cheaper than on disk/flash, but still expensive compared to cache read
- Binary search for a key value within a large B+-tree node results in many cache misses
二分查找可能带来很多 cache miss. - Data structures that make best use of cache preferable – cache conscious
B+- trees with small nodes that fit in cache line are preferable to reduce cache misses
search key 和 pointer 可以分开放。
Key idea:
- use large node size to optimize disk access,
- but structure data within a node using a tree with small node size, instead of using an array, to optimize cache access.

Indexing on Flash#
Flash 里不是即时修改,而是先擦掉再写。同时擦的次数是有限制的。因此最好的方法是从底构建,然后顺序写入。
- Random I/O cost much lower on flash
20 to 100 microseconds for read/write - Writes are not in-place, and (eventually) require a more expensive erase Optimum page size therefore much smaller
- Bulk-loading still useful since it minimizes page erases
- Write-optimized tree structures (i.e., LSM-tree) have been adapted to minimize page writes for flash-optimized search trees
写优化索引结构
Log Structured Merge (LSM) Tree#
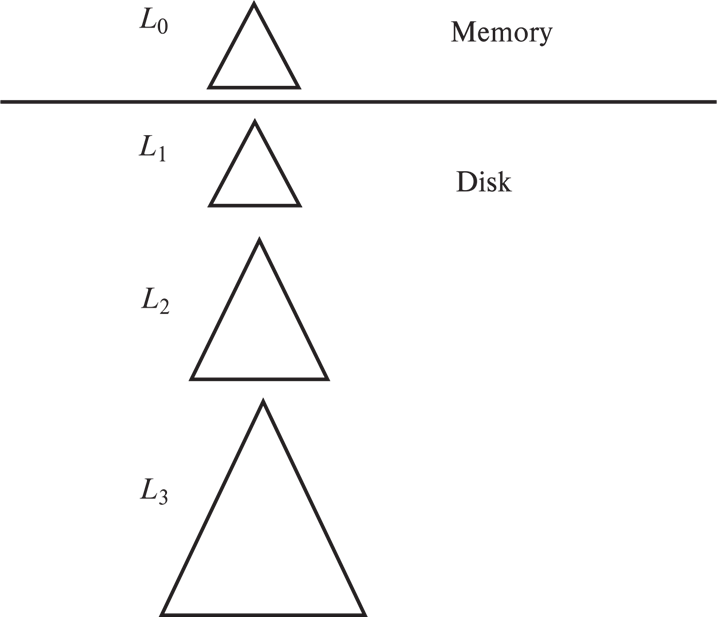
- Records inserted first into in-memory tree (\(L_0\) tree)
- When in-memory tree is full, records moved to disk (\(L_1\) tree)
B+-tree constructed using bottom-up build by merging existing \(L_1\) tree with records from \(L_0\) tree
内存里的 B+ 树如果满了,就马上写到磁盘里去(可以连续写) - When \(L_1\) tree exceeds some threshold, merge into \(L_2\) tree
And so on for more levels
Size threshold for \(L_{i+1}\) tree is \(k\) times size threshold for \(L_i\) tree
这样我们把随机写变为了顺序写。但此时查找一个索引,就要遍历所有 B+ 树。
- Benefits of LSM approach
- Inserts are done using only sequential I/O operations
- Leaves are full, avoiding space wastage
- Reduced number of I/O operations per record inserted as compared to normal B+-tree (up to some size)
- Drawback of LSM approach
- Queries have to search multiple trees
- Entire content of each level copied multiple times
Stepped Merge Index
原先的结构中,Merge 操作太多,我们可以一次性合并。
磁盘上每层有 k 棵树,当 k 个索引处于同一层时,合并它们并得到一棵层数 \(+1\) 的树,写回。
\(L_1\) 有大小限制,达到后会生成另一个 B+ 树,依次为 k 倍。
布隆过滤器
Created: 2024年3月19日 11:22:29