Basic Method#

摘要

目录资源

Basic Method

1. 决策树和随记森林#

1.1.1 decision tree classification#

机器学习中的决策树就好似搜索树一样（请与fds中学到的决策树区分），能够对非线性分割的目标进行逐步拆分。如图：

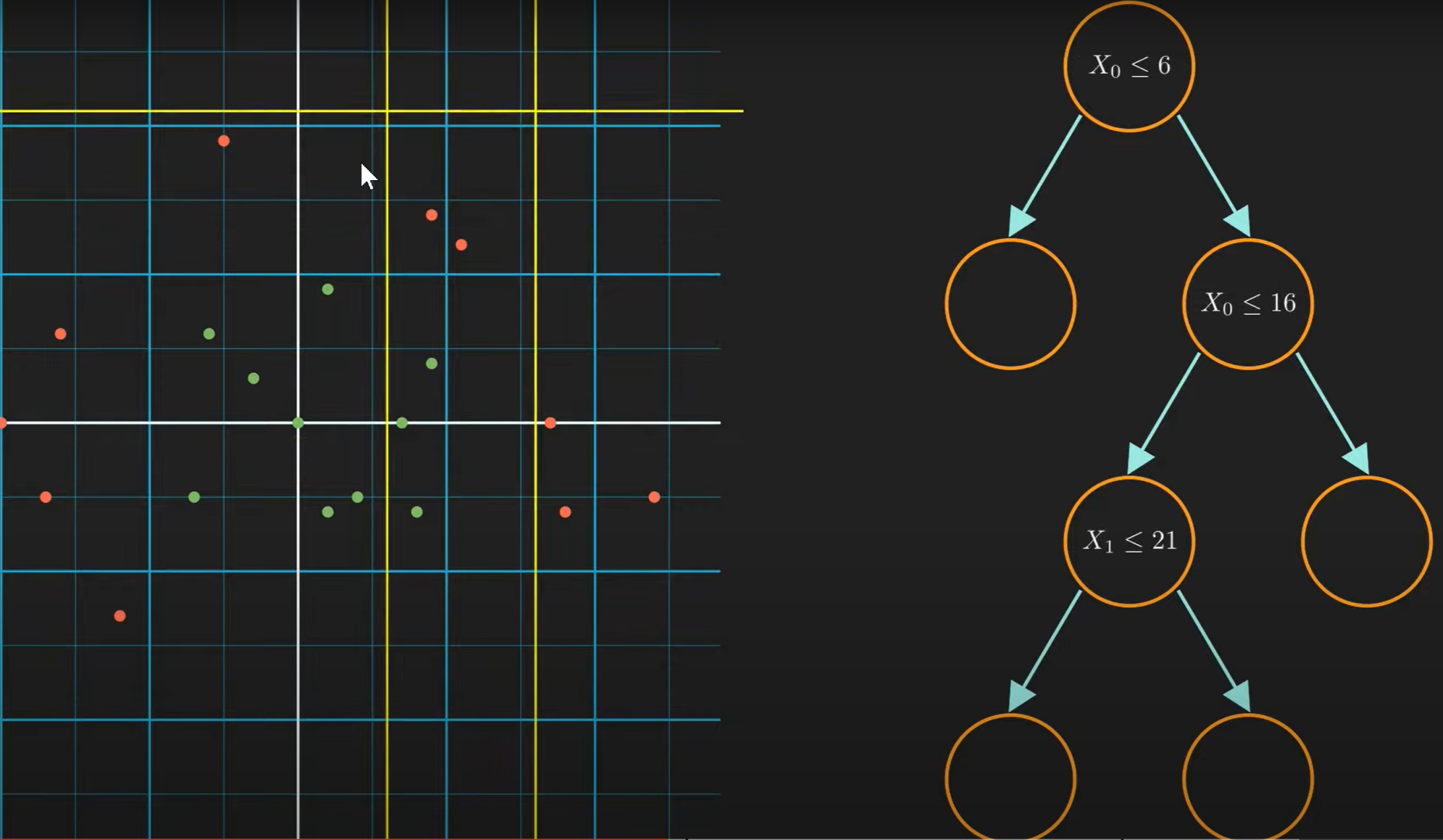
而当我们探讨，$\text{which split is better?}$ 这个问题的时候, 我们需要information gain和 entropy两个概念

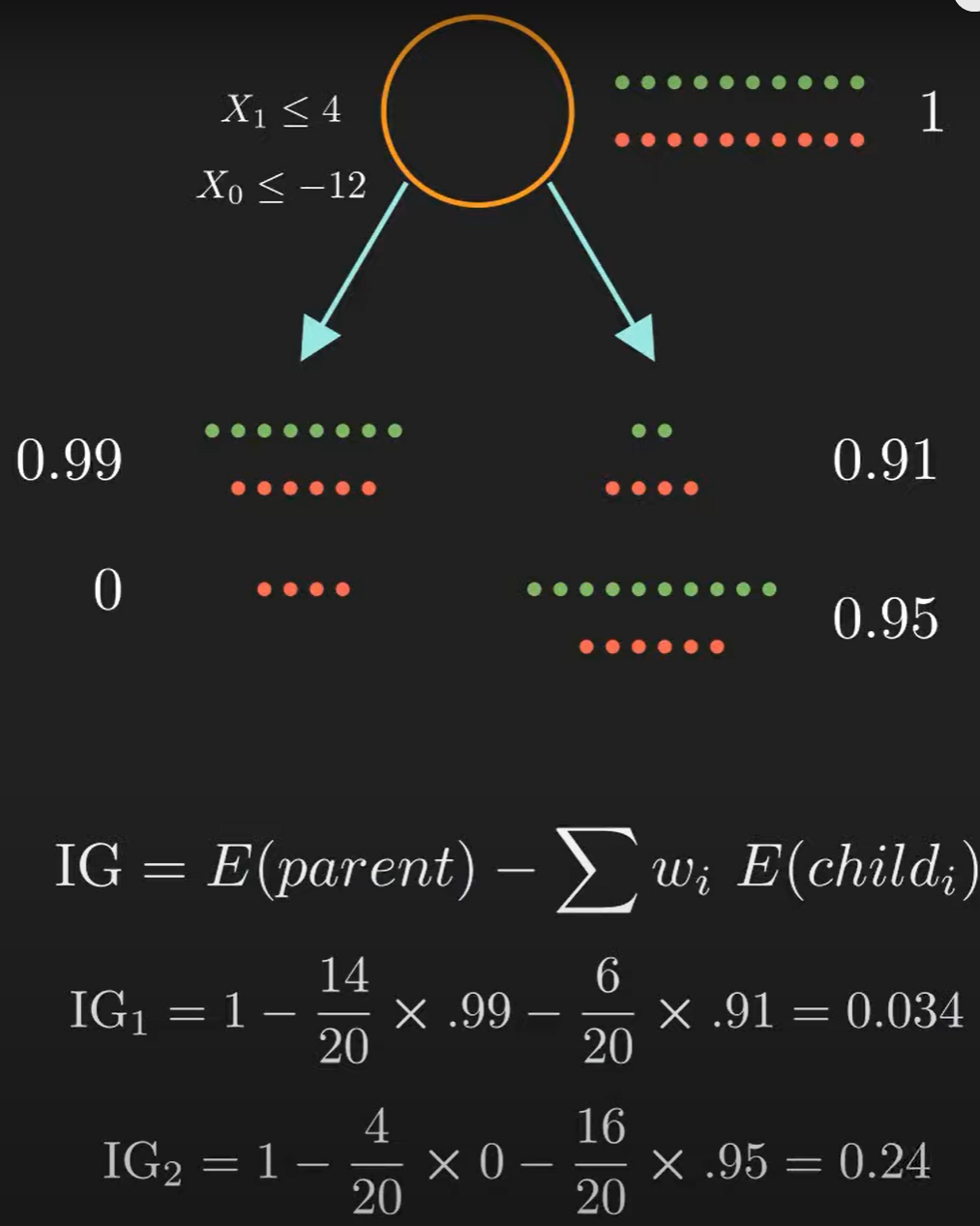
\[ Entropy = \sum{-p_i log(p_i)} \\ IG = E(parent) - \sum w_i E(child) \]

由此我们便可以计算出哪种分类方式更好。最后，我们确保每个叶节点都只要单一类型的元素。

代码建议阅读源码看看！

1.1.2 decision tree regression#

决策树回归的原理与分类类似，只是我们需要用到MSE来计算IG，并且最后的叶节点不再是单一类型的元素，而是一个平均值。（小结：regression更偏向解决连续连续型的问题，而classification更偏向解决离散型的问题） $$ Var = \frac{1}{n} \sum (y_i - \hat{y_i})^2 $$ 为了使叶节点更纯净，我们要让方差尽可能小。因此，我们需要找到一个最优的切分点，使得切分后的两个子集的方差之和最小。与上面IG的计算相似： $$ Var_{target} = Var_{parent} - \sum w_i Var_{child} $$

这个问题还可以通过遍历所有的特征和特征值来解决，但是这样的时间复杂度太高，因此我们可以通过随机选取特征和特征值来解决这个问题。这就是随机森林的原理。

1.2.1 random forest classification#

随机森林是一种集成学习方法，它通过集成多个决策树来解决分类问题。它的原理是通过随机选取特征和特征值（Bootstrapping & Feature Selection）来构建多个决策树，然后通过投票的方式来决定最终的分类结果。这样做的好处是，既能够减少过拟合，又能够减少计算量。

两个随记过程： 1. Bootstrapping：保证每个树使用不同的数据，让模型对原始数据的分布不敏感。 2. Feature Selection：保证每个树使用不同的特征，让模型对特征的选择不敏感，减少了不同树之间的相关性。

伪代码如下：
def fit(self, X, y):
    for i in range(self.n_estimators):
        X_subset, y_subset = self._get_random_subsets(X, y)
        tree = DecisionTree()
        tree.fit(X_subset, y_subset)
        self.trees.append(tree)

小结

研究发现，特征子集的个数接近$\sqrt{m}$或者$log^{m}$时，模型的性能最好(其中，$m$是特征的个数)。
用于regression时，我们可以用平均值来代替投票的方式。

2. Markov#

2.1.1 Markov Chain#

这是一个经典的概率推断模型，其中观看Normal Nerd的视频你将会有个清晰的认知。这里我只是简单的记录一下。

高阶转移矩阵和特征值求稳定概率分布的方法。

2.1.2 Hidden Markov Model#

2.1.3 HMM：Forward Algorithm#

2.2.1 Markov Decision Process#

这是一个经典的强化学习模型。

2.2.2 Q-Learning#

2.2.3 Deep Q-Learning#

3. SVM#

SVM是一种监督学习算法，它的目标是找到一个超平面，将不同类别的数据分开。

Last update: 2023年12月12日 22:41:49
Created: 2023年12月10日 14:41:44